Equations, inéquations du second degré.
Introduction.
- Conjecturer quant au nombre de solution(s) pour l'équation $f(x)=0$.
- Montrer que pour tout $x\in\mathbb{R}$ on a: $f(x)=2\bigg[(x-\dfrac{3}{4})^2-\dfrac{17}{16}\bigg]$.
- Factoriser $2\bigg[(x-\dfrac{3}{4})^2-\dfrac{17}{16}\bigg]$.
- Résoudre algébriquement l'équation $2x^2-3x-1=0$.
- Résoudre $f(x)=0$, revient a regarder les points d'intersection de la courbe $\mathcal{C}_f$ et l'axe des abscisse. On remarue qu'il y a donc deux solution possible.
- $f(x)=2\bigg[\bigg(x-\dfrac{3}{4}\bigg)^2-\dfrac{17}{16}\bigg]$ $=2\bigg[\bigg(x^2-2\times x\times\dfrac{3}{4}+(\dfrac{3}{4})^2\bigg)-\dfrac{17}{16}\bigg]$ $=2\bigg[\bigg(x^2-\dfrac{3}{2}\times x+\dfrac{9}{16}\bigg)-\dfrac{17}{16}\bigg]$ $=2\bigg[x^2-\dfrac{3}{2}\times x-\dfrac{1}{2}\bigg]$ $=2x^2-3x-1$.
- $2\bigg[(x-\dfrac{3}{4})^2-\dfrac{17}{16}\bigg]$ $=2\bigg[(x-\dfrac{3}{4})-\sqrt{\dfrac{17}{16}}\bigg]\times\bigg[(x-\dfrac{3}{4})+\sqrt{\dfrac{17}{16}}\bigg]$ $=2\bigg[(x-\dfrac{3}{4})-\dfrac{\sqrt{17}}{4}\bigg]\times\bigg[(x-\dfrac{3}{4})+\dfrac{\sqrt{17}}{4}\bigg]$.
- $2\bigg[(x-\dfrac{3}{4})-\dfrac{\sqrt{17}}{4}\bigg]\times\bigg[(x-\dfrac{3}{4})+\dfrac{\sqrt{17}}{4}\bigg]=0$
$\Leftrightarrow$ $\bigg[(x-\dfrac{3}{4})-\dfrac{\sqrt{17}}{4}\bigg]=0$ ou $\bigg[(x-\dfrac{3}{4})+\dfrac{\sqrt{17}}{4}\bigg]=0$.
Donc:- $x=\dfrac{3}{4}+\dfrac{\sqrt{17}}{4}=\dfrac{3+\sqrt{17}}{4}$
- ou bien $x=\dfrac{3}{4}-\dfrac{\sqrt{17}}{4}=\dfrac{3-\sqrt{17}}{4}$.
Forme canonique d'un trinôme du second degré.
- Si on pose $\alpha=-\dfrac{b}{2a}$ et,
- $\beta=-\dfrac{\Delta}{4a}$
 $P(x)=x^2+x+1$
$P(x)=x^2+x+1$ $Q(x)=5x^2+3x-1$
$Q(x)=5x^2+3x-1$- $P(x)=$$x^2+x$$+1$ $=(x+\dfrac{1}{2})^2-\dfrac{1}{4}$$+1$ $=(x+\dfrac{1}{2})^2+\dfrac{3}{4}$.
- $Q(x)=$$5x^2+3x$$-1$ $=(x+\dfrac{3}{10})^2-\dfrac{9}{100}$$-1$ $=(x+\dfrac{3}{10})^2-\dfrac{109}{100}$.
Equation du second degré.
- Si $\Delta>0$, alors $P$ admet deux racines réelles distinctes:
$x_0=\dfrac{-b-\sqrt{\Delta}}{2a}$ et $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$. et pour tout $x\in\mathbb{R}$, on a $P(x)=a(x-x_0)(x-x_1)$. - Si $\Delta=0$, alors $P$ admet une seule racine réelle (racine double):
$x_0=\dfrac{-b}{2a}.$ et pour tout $x\in\mathbb{R}$, on a $P(x)=a(x-x_0)^2$. - Si $\Delta<0$, alors $P$ n'admet pas de racines réelles et on ne peut pas factoriser $P(x)$.
- Résoudre l'équation $f(x)=0$
- Donner le tableau de signes de la fonction $f$.
- Factoriser $f(x)$.
- $ax^2+bx+c=a\bigg(x^2+\displaystyle\frac{b}{a}x+\displaystyle\frac{c}{a}\bigg)$ $=a\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2-\displaystyle\frac{b^2}{4a^2}+\displaystyle\frac{c}{a}\bigg)$ $=a\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2-\displaystyle\frac{b^2}{4a^2}+\displaystyle\frac{4ac}{4a^2}\bigg)$
- Si $\Delta>0$
- Si $\Delta=0$
- Si $\Delta<0$ On a $ax^2+bx+c=a\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2-\displaystyle\frac{\Delta}{4a^2}\bigg)$
Si on pose $\beta=-\displaystyle\frac{\Delta}{4a^2}$, on remarque que $\beta>0$ et $ax^2+bx+c=a\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2+\beta\bigg)$.
Comme $\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2\geq 0$ et $\beta>0$, nous avons que pour tout $x\in\mathbb{R}$, $\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2+\beta\bigg)>0$.
Donc pour tout $x\in\mathbb{R}$ a $\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2-\displaystyle\frac{\Delta}{4a^2}\bigg)\not=0$, puisque $a\not=0$.
$P$ n'admet pas de racines réelles et on ne peut pas factoriser $P(x)$.  $x^2-x-6=0$
$x^2-x-6=0$ $16x^2+8x+1=0$
$16x^2+8x+1=0$ $x^2+x+1=0$
$x^2+x+1=0$- Résolution de l'équation : $x^2-x-6=0$, on a $a=1$, $b=-1$ et $c=-6$.
$\Delta=b^2-4ac=(-1)^2-4\times 1\times(-6)=1+24=25>0$, alors l'équation admet deux solutions réelles distinctes:
$x_0=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-(-1)-\sqrt{25}}{2}=-2$ et $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-(-1)+\sqrt{25}}{2}=3$. - Résolution de l'équation : $16x^2+8x+1=0$, on a $a=16$, $b=8$ et $c=1$.
$\Delta=b^2-4ac=8^2-4\times 16\times 1=0$, alors l'équation admet une seule racine réelle (racine double):
$x_0=\dfrac{-b}{2a}=\dfrac{-8}{32}=-\dfrac{1}{4}$.Remarque.
On aurait pu résoudre cette équation en remarquant que $16x^2+8x+1$ est une identité remarquable, en effet
$16x^2+8x+1=(4x+1)^2$, donc $16x^2+8x+1=0$ $\Leftrightarrow$ $(4x+1)^2=0$ $\Leftrightarrow$ $(4x+1)=0$ $\Leftrightarrow$ $x=-\dfrac{1}{4}$. - Résolution de l'équation : $x^2+x+1=0$, on a $a=1$, $b=1$ et $c=1$.
$\Delta=b^2-4ac=(1)^2-4\times 1\times 1=-3 < 0$, alors l'équation n' admet pas de solution réelle . Signe d'un trinôme du second degré, inéquation du second degré.
- Si $\Delta>0$, et si $x_0$ et $x_1$ désignent les racines de $P$, avec $x_0 < x_1$, alors
$P(x)$ est du signe de $a$ si et seulement si $x\in]-\infty;x_0[\cup]x_1;+\infty[$.
On dit aussi que $P(x)$ est du signe de $a$ en dehors des racines.$~~~~~~~~$
- Si $\Delta=0$ alors
$P(x)$ est du signe de $a$ si et seulement si $x\not=\displaystyle\frac{-b}{2a}$.$~~~~~~~~$

- Si $\Delta<0$ alors $P(x)$ est du signe de $a$ pour tout $x\in\mathbb{R}$.$~~~~~~~~$

Pour rappel:
Donc $ax^2+bx+c=a\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2-\displaystyle\frac{b^2-4ac}{4a^2}\bigg)$. Posons $\Delta=b^2-4ac$. Trois cas se posent.- Si $\Delta>0$
$ax^2+bx+c=a\bigg(x+\displaystyle\frac{b-\sqrt{\Delta}}{2a}\bigg)\bigg(x+\displaystyle\frac{b+\sqrt{\Delta}}{2a}\bigg)$.- $\bigg(x+\displaystyle\frac{b-\sqrt{\Delta}}{2a}\bigg)>0$ $\Leftrightarrow$ $x>-\displaystyle\frac{b-\sqrt{\Delta}}{2a}=\dfrac{-b+\sqrt{\Delta}}{2a}$.
- $\bigg(x+\displaystyle\frac{b+\sqrt{\Delta}}{2a}\bigg)>0$ $\Leftrightarrow$ $x>-\displaystyle\frac{b+\sqrt{\Delta}}{2a}=\dfrac{-b-\sqrt{\Delta}}{2a}$.

- Si $\Delta=0$
On a $ax^2+bx+c=a(x+\displaystyle\frac{b}{2a})^2$.
Pour tout $x\in\mathbb{R}$ on a $(x+\displaystyle\frac{b}{2a})^2\geq 0$, donc:
le signe de $a(x+\displaystyle\frac{b}{2a})^2$ = signe de $a$.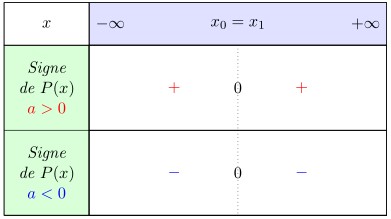
- Si $\Delta<0$ On a $ax^2+bx+c=a\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2-\displaystyle\frac{\Delta}{4a^2}\bigg)$
Si on pose $\beta=-\displaystyle\frac{\Delta}{4a^2}$, on remarque que $\beta>0$ et $ax^2+bx+c=a\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2+\beta\bigg)$.
Comme $\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2\geq 0$ et $\beta>0$, nous avons que pour tout $x\in\mathbb{R}$, $\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2+\beta\bigg)>0$.
Donc pour tout $x\in\mathbb{R}$ a $\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2-\displaystyle\frac{\Delta}{4a^2}\bigg)\not=0$, puisque $a\not=0$.
$P$ n'admet pas de racines réelles.
le signe de $a\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2-\displaystyle\frac{\Delta}{4a^2}\bigg)$= signe de $a$.
Inéquations du second degré.
- Résoudre algébriquement l'inéquation $f(x)>g(x)$.
- Retrouver le résultat graphiquement.
Nous avons: $f(x)>g(x)$ $\Leftrightarrow$ $x^2-1>2x+1$ $\Leftrightarrow$ $x^2-2x-2>0$.
Etudions le signe du trinome $x^2-2x-2$, on a $a=1$, $b=-2$ et $c=-2$.
$\Delta=b^2-4ac=(-2)^2-4\times 1\times (-2)=4+8=12>0$. Calculons les racines de $x^2-2x-2$.
$x_0=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-(-2)-\sqrt{12}}{2}$ et $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-(-2)+\sqrt{12}}{2}$, comme $\sqrt{12}=2\sqrt{3}$.
Donc $x_0=1-\sqrt{3}$ et $x_1=1+\sqrt{3}$.
Nous savons que $x^2-2x-2>0$ pour tout $x\in]-\infty;1-\sqrt{3}[\cup ]1+\sqrt{3};+\infty[$. Nous avons donc le tableau de signes ci-contre.
Grâce au tableau de signes de $f(x)-g(x)=x^2-2x-2$, nous avons $f(x)>g(x)$ $\Leftrightarrow$ $x\in]-\infty;1-\sqrt{3}[\cup ]1+\sqrt{3};+\infty[$.
- Résoudre graphiquement l'équation $f(x)>g(x)$, revient à regarder quand la courbe de $f$ est au dessus de la courbe de $g$.
Variations des fonctions polynômiales de degré 2.
- $f$ est croissante sur l'intervalle $[-\dfrac{b}{2a};+\infty[$.
- $f$ est décroissante sur l'intervalle $]-\infty;-\dfrac{b}{2a}]$.
- $f$ amet un minimum égal à $-\dfrac{\Delta}{4a}$ atteint pour $x=-\dfrac{b}{2a}$.
- $f$ est strictement décroissante sur l'intervalle $[-\dfrac{b}{2a};+\infty[$.
- $f$ est strictement croissante sur l'intervalle $]-\infty;-\dfrac{b}{2a}]$.
- $f$ amet un maximum égal à $-\dfrac{\Delta}{4a}$ atteint pour $x=-\dfrac{b}{2a}$.
- Cas: $a>0$.
- Soit $t,t'\in[-\dfrac{b}{2a};+\infty[$, avec $t < t'$, $\Rightarrow$ $0 \leq \bigg[t+\displaystyle\frac{b}{2a}\bigg] < \bigg[t'+\displaystyle\frac{b}{2a}\bigg]$.
$\Rightarrow$ $\bigg[t+\displaystyle\frac{b}{2a}\bigg]^2 < \bigg[t'+\displaystyle\frac{b}{2a}\bigg]^2$, donc on a:
$\bigg[t+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2} < \bigg[t'+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}$, or $a>0$.
$\Rightarrow$ $a\bigg(\bigg[t+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}\bigg) < a\bigg(\bigg[t'+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}\bigg)$ $\Rightarrow$ $f(t) < f(t')$, donc $f$ est croissante sur l'intervalle $[-\dfrac{b}{2a};+\infty[$. - Soit $t,t'\in]-\infty;-\dfrac{b}{2a}]$, avec $t < t'$, $\Rightarrow$ $ \bigg[t+\displaystyle\frac{b}{2a}\bigg] < \bigg[t'+\displaystyle\frac{b}{2a}\bigg]\leq 0$.
$\Rightarrow$ $\bigg[t+\displaystyle\frac{b}{2a}\bigg]^2 > \bigg[t'+\displaystyle\frac{b}{2a}\bigg]^2$, donc on a:
$\bigg[t+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2} > \bigg[t'+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}$, or $a>0$.
$\Rightarrow$ $a\bigg(\bigg[t+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}\bigg) > a\bigg(\bigg[t'+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}\bigg)$ $\Rightarrow$ $f(t) > f(t')$, donc $f$ est décroissante sur l'intervalle $[-\infty;-\dfrac{b}{2a}]$.
- Soit $t,t'\in[-\dfrac{b}{2a};+\infty[$, avec $t < t'$, $\Rightarrow$ $0 \leq \bigg[t+\displaystyle\frac{b}{2a}\bigg] < \bigg[t'+\displaystyle\frac{b}{2a}\bigg]$.
- Cas: $a < 0$.
- Soit $t,t'\in[-\dfrac{b}{2a};+\infty[$, avec $t < t'$, $\Rightarrow$ $0 \leq \bigg[t+\displaystyle\frac{b}{2a}\bigg] < \bigg[t'+\displaystyle\frac{b}{2a}\bigg]$.
$\Rightarrow$ $\bigg[t+\displaystyle\frac{b}{2a}\bigg]^2 < \bigg[t'+\displaystyle\frac{b}{2a}\bigg]^2$, donc on a:
$\bigg[t+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2} < \bigg[t'+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}$, or $a < 0$.
$\Rightarrow$ $a\bigg(\bigg[t+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}\bigg) > a\bigg(\bigg[t'+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}\bigg)$ $\Rightarrow$ $f(t)> f(t')$, donc $f$ est décroissante sur l'intervalle $[-\dfrac{b}{2a};+\infty[$. - Soit $t,t'\in]-\infty;-\dfrac{b}{2a}]$, avec $t < t'$, $\Rightarrow$ $ \bigg[t+\displaystyle\frac{b}{2a}\bigg] < \bigg[t'+\displaystyle\frac{b}{2a}\bigg]\leq 0$.
$\Rightarrow$ $\bigg[t+\displaystyle\frac{b}{2a}\bigg]^2 > \bigg[t'+\displaystyle\frac{b}{2a}\bigg]^2$, donc on a:
$\bigg[t+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2} > \bigg[t'+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}$, or $a < 0$.
$\Rightarrow$ $a\bigg(\bigg[t+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}\bigg) < a\bigg(\bigg[t'+\displaystyle\frac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}\bigg)$ $\Rightarrow$ $f(t) < f(t')$, donc $f$ est croissante sur l'intervalle $[-\infty;-\dfrac{b}{2a}]$.
- Soit $t,t'\in[-\dfrac{b}{2a};+\infty[$, avec $t < t'$, $\Rightarrow$ $0 \leq \bigg[t+\displaystyle\frac{b}{2a}\bigg] < \bigg[t'+\displaystyle\frac{b}{2a}\bigg]$.
Somme et produit des racines d'un trinôme du second degré.
- $x_0+x_1=\dfrac{-b}{a}$.
- $x_0\times x_1=\dfrac{c}{a}$.
- $P(\dfrac{x_0+x_1}{2})=\dfrac{-\Delta}{4a}$.
- Si $\Delta>0$
$ax^2+bx+c=a(x-x_0)(x-x_1)=ax^2-a(x_0+x_1)x+ax_0x_1$ pour tout $x\in\mathbb{R}$ $\Leftrightarrow$ $-a(x_0+x_1)=b$ et $c=ax_0x_1$.
Donc $x_0+x_1=\dfrac{-b}{a}$ et $x_0\times x_1=\dfrac{c}{a}$. - Si $\Delta=0$
$x_0=x_1$, on retrouve aussi que $x_0+x_1=\dfrac{-b}{a}$ et $x_0\times x_1=\dfrac{c}{a}$.
- Si $\Delta>0$
- Nous savons que $x_0+x_1=\dfrac{-b}{a}$, donc $\dfrac{x_0+x_1}{2}=-\dfrac{b}{2a}$.
Nous savons aussi que pour tout $x\in\mathbb{R}$, $P(x)=ax^2+bx+c=a\bigg(\bigg[x+\dfrac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}\bigg)$.
Donc $P(\dfrac{x_0+x_1}{2})=a\bigg(\bigg[(-\dfrac{b}{2a}+\dfrac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}\bigg)=\dfrac{-\Delta}{4a}$ Savoir reconnaître une fonction du second degré par sa courbe.
- Le signe de $a$ donne une indication sur l'orientation des branches de la parabole.
- Le signe de $\Delta$ donne une indication sur le nombre de points d'intersection entre $\mathcal{C}_f$ et l'axe $(ox)$.
- Les coordonnées du sommet $S(\dfrac{-b}{2a};\dfrac{-\Delta}{4a})$.
- L'ordonnée à l'origine $f(0)=c$, donne aussi une bonne indication de position.
Equations bicarrées.
- On peut conjecturer qu'il y a 4 solutions pour l'équetion $f(x)=0$.
- Résolvons l'équation du second degré $\theta^2-3\theta+2=0$.
$\Delta=(-3)^2-4\times 1\times 2=9-8=1>0$, donc l'équation $\theta^2-3\theta+2=0$ admet deux solutions réelles distinctes.
$x_0=\dfrac{-(-3)-\sqrt{1}}{2}=1$ et $x_1=\dfrac{-(-3)+\sqrt{1}}{2}=2$. - Posons $\theta=x^2$, on a donc l'équivalence:
$x^4-3x^2+2=0$ $\Leftrightarrow$ $\theta^2-3\theta+2=0$.
Donc on a $x^2=1$ ou $x^2=2$ $\Leftrightarrow$ ($x=1$ ou $x=-1$) ou ($x=\sqrt{2}$ ou $x=-\sqrt{2}$).
On écrit si $S$ représente l'ensemble des solutions de $f(x)=0$, $S=\{-\sqrt{2};-1;1;\sqrt{2}\}$. - Conjecturer quant au nombre de solution(s) pour l'équation $f(x)=0$.
- Résoudre Dans $\mathbb{R}$ l'équation $\theta^2-3\theta+2=0$.
- En posant $\theta=x^2$, donner les solutions exactes de l'équation $x^4-3x^2+2=0$.
Exercice.
Soit la fonction définie sur $\mathbb{R}$ par $f(x)=2x^2-3x-1$.
Voici ci-contre $\mathcal{C}_f$ la courbe représentative de $f$.
Courbe $\mathcal{C}_f$.

Théorème.
Tout trinôme du second degré $P(x)=ax^2+bx+c$, avec $a\not=0$, s'écrit de façon unique sous la forme:
$a(x-\alpha)^2+\beta$.
L'écriture $a(x-\alpha)^2+\beta$ est appelée la forme canonique du trinôme $P$.
Donc $ax^2+bx+c=a\bigg(\bigg[x+\dfrac{b}{2a}\bigg]^2-\displaystyle\frac{b^2-4ac}{4a^2}\bigg)$. Posons $\Delta=b^2-4ac$.
Donc $ax^2+bx+c=a\bigg(\bigg[x+\dfrac{b}{2a}\bigg]^2-\dfrac{\Delta}{4a^2}\bigg)$
Définition.
Soit $ax^2+bx+c$ un trinôme du second degré avec $a\not=0$.
On appelle discriminant du trinôme, le réel noté $\Delta$ défini par:
$\Delta=b^2-4ac$.
Exemples.
Donner la forme canonique de:Théorème.
Soit $P(x)=ax^2+bx+c$, avec $a\not=0$, considérons l'équation $P(x)=0$.
Exercice.
; Soit $f(x)=$ $x^2$+x+Donc $ax^2+bx+c=a\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2-\displaystyle\frac{b^2-4ac}{4a^2}\bigg)$. Posons $\Delta=b^2-4ac$. Trois cas se posent.
On peut écrire $ax^2+bx+c=a\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]^2-\displaystyle\frac{\Delta}{4a^2}\bigg)$ $=a\bigg(\bigg[x+\displaystyle\frac{b}{2a}\bigg]-\displaystyle\frac{\sqrt{\Delta}}{2a}\bigg)(\bigg[x+\displaystyle\frac{b}{2a}\bigg]+\displaystyle\frac{\sqrt{\Delta}}{2a}\bigg)$ $=a\bigg(x+\displaystyle\frac{b-\sqrt{\Delta}}{2a}\bigg)\bigg(x+\displaystyle\frac{b+\sqrt{\Delta}}{2a}\bigg)$.
Donc $P(x)=ax^2+bx+c$ admet deux racines réelles distinctes. $x_0=\dfrac{-b-\sqrt{\Delta}}{2a}$ et $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$.
On a $ax^2+bx+c=a(x+\displaystyle\frac{b}{2a})^2$, donc $P(x)$ admet une racine réelle double $x_0=\displaystyle\frac{-b}{2a}.$
Exemples.
Résoudre les équations du second degré suivantes.
Théorème.
Soit $P$ la fonction trinôme du second degré définie sur $\mathbb{R}$ par:
$P(x)=ax^2+bx+c$, avec $a,b,c\in\mathbb{R}$ et $a\not=0$.
Soit $\Delta=b^2-4ac$ le discriminant de $P$.
 |
Définition.
On appelle inéquation du second degré toute inéquation de la forme:
$ax^2+bx+c < 0$ ou $ax^2+bx+c>0$ ou $ax^2+bx+c\leq0$ ou $ax^2+bx+c\geq0$
où $a,b,c\in\mathbb{R}$ avec $a\not=0$.
Exercice.
Soit la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=x^2-1$, et soit la fonction $g$ définie sur $\mathbb{R}$ par $g(x)=2x+1$.
Courbes de $\mathcal{C}_f$ et $\mathcal{C}_g$.

Théorème.
Soit $f$ la fonction trinôme du second degré définie sur $\mathbb{R}$ par: $f(x)=ax^2+bx+c$, avec $a,b,c\in\mathbb{R} $et $a\not=0$. Le sens de variation de la fonction $f$ dépend du signe de $a$ on a:


Théorème.
Soit $P(x)=ax^2+bx+c$ un trinôme du second degré, si $\Delta\geq 0$. on les relation suivantes:
Propriété admise en première.
Soit $P(x)=ax^2+bx+c$ et $Q(x)=a'x^2+b'x+c'$ deux fonction trinômes du second degré.
$P(x)=Q(x)$ pour tout $x\in\mathbb{R}$ $\Leftrightarrow$ $a=a'$; $b=b'$ et $c=c'$.
Cliquer sur la courbe qui correspond à la fonction f, donnée ci
|
Exercice.
Soit $f$ la fonction définie pour tout $x\in\mathbb{R}$ par $f(x)=x^4-3x^2+2$ Voici ci-contre $\mathcal{C}_f$ la courbe représentative de $f$.
Courbe $\mathcal{C}_f$.
