Equations cartésiennes d'une droite.
Vecteurs colinéaires(rappels).
Equations de droites de la forme $ax+by+c=0$.
Considérons la droite $(\mathcal{D})$ passant par $A(x_0;y_0)$ et de vecteur directeur $\overrightarrow{u}\begin{pmatrix} -b\\ a \\ \end{pmatrix}$. Soit Un point M(x;y) quelconque du plan munit du repère $\mathcal{R}=(O;\overrightarrow{i};\overrightarrow{j})$.
Nous avons les assertions suivantes équivalentes:
$M(x;y)\in(\mathcal{D})$ $\Leftrightarrow$ les vexteurs $\overrightarrow{AM}$ et $\overrightarrow{u}\begin{pmatrix} -b\\ a \\ \end{pmatrix}$ sont colinéaires. $\Leftrightarrow$ $\det(\overrightarrow{u},\overrightarrow{v})=0$ $\Leftrightarrow$ $\begin{array}{|cc|} x-x_0&-b\\ y-y_0&a\\ \end{array}=0$ $\Leftrightarrow$ $a(x-x_0)-(-b)(y-y_0)=0$ $\Leftrightarrow$ $ax+by+(-ax_0-by_0)=0$. Les nombre $a$, $b$, $x_0$ et $y_0$ sont donnés par défintion de la droite $(\mathcal{D})$. Posons pour simplifier les notation $c=(-ax_0-by_0)$.
Nous avons donc l'équivalence: $M(x;y)\in(\mathcal{D})$ $\Leftrightarrow$ $ax+by+c=0$.Remarque.
L' équivalence: $M(x;y)\in(\mathcal{D})$ $\Leftrightarrow$ $ax+by+c=0$, veut simplement dire que nous possédons un test algébrique ici $ax+by+c=0$ pour savoir si oui ou non un point $M(x;y)$ appartient à $(\mathcal{D})$.
La relation $ax+by+c=0$ s'appelle l' équation réduite de $(\mathcal{D})$.La démonstration de la réciproque n'est pas au programme de la seconde.
- Toute droite de vecteur directeur $\overrightarrow{u}(-b;a)$ admet pour équation, une équation de la forme: $ax+by+c=0$.
- Inversement, l'ensemble des points $M(x;y)$ tels que $ax+by+c=0$, avec $(a;b)\not=(0;0)$, est une droite de vecteur directeur de coordonnées $\overrightarrow{u}(-b;a)$.
- $\Delta$ passe par $A(-3;2)$ et $B(2;5)$.
- $\Delta$ passe par $A(-1;2)$ et ayant pour vecteur directeur $\overrightarrow{u}\begin{pmatrix}1\\-2\\ \end{pmatrix}$.
- $\Delta$ passe par $A(2;-1)$ et est parallèle à la droite $(d)$ d'équation cartésienne $x-2y-3=0$.
- Calculons les coordonnées du vacteur $\overrightarrow{AB}$, on a $\overrightarrow{AB}\begin{pmatrix}x_B-x_A\\y_B-y_A\\ \end{pmatrix}\begin{pmatrix}2-(-3)\\5-2\\ \end{pmatrix}
\begin{pmatrix}5\\3\\ \end{pmatrix}$.
$M(x;y)\in\Delta$ $\Leftrightarrow$ les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires $\Leftrightarrow$ $\det(\overrightarrow{AM},\overrightarrow{AB})=0$ $\Leftrightarrow$ $\begin{array}{|cc|}x-(-3)&5\\y-2&3\\ \end{array}=0$ $\Leftrightarrow$ $\begin{array}{|cc|}x+3&5\\y-2&3\\ \end{array}=0$ $\Leftrightarrow$ $3(x+3)-5(y-2)=0$ $\Leftrightarrow$ $3x-5y+19=0$.
Une équation cartésienne possible de $\Delta$ est $3x-5y+19=0$, on note cela $\Delta:3x-5y+19=0$. - $M(x;y)\in\Delta$ $\Leftrightarrow$ les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{u}\begin{pmatrix}1\\-2\\ \end{pmatrix}$ sont colinéaires.
$\det(\overrightarrow{AM},\overrightarrow{u})=0$ $\Leftrightarrow$ $\begin{array}{|cc|}x-(-1)&1\\y-2&-2\\ \end{array}=0$ $\Leftrightarrow$ $\begin{array}{|cc|}x+1&1\\y-2&-2\\ \end{array}=0$ $\Leftrightarrow$ $-2(x+1)-(y-2)=0$ $\Leftrightarrow$ $-2x-y=0$.
Une équation cartésienne possible de $\Delta$ est $2x+y=0$, on note cela $\Delta:2x+y=0$. - La droite $(d)$ d'équation cartésienne $x-2y-3=0$ a pour vecteur directeur $\overrightarrow{u}\begin{pmatrix}2\\1\\ \end{pmatrix}$.
$M(x;y)\in\Delta$ $\Leftrightarrow$ les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{u}\begin{pmatrix}2\\1\\ \end{pmatrix}$ sont colinéaires.
$\det(\overrightarrow{AM},\overrightarrow{u})=0$ $\Leftrightarrow$ $\begin{array}{|cc|}x-2&2\\y-(-1)&1\\ \end{array}=0$ $\Leftrightarrow$ $\begin{array}{|cc|}x-2&2\\y+1&1\\ \end{array}=0$ $\Leftrightarrow$ $(x-2)-2(y+1)=0$ $\Leftrightarrow$ $x-2y-4=0$.
Equation réduite d'une droite.
Propriétes.
Soit $\Delta$ une droite du plan ayant un repère $(O;\vec{i};\vec{j})$.
- Si $\Delta$ est non parallèle à l'axe des ordonnées; une équation de $\Delta$ est de la forme $y=mx+p$, cette équation s'appelle équation réduite de $\Delta$.
- Si $\Delta$ est parallèle à l'axe des ordonnées. Une équation de $\Delta$ est de la forme $x=c$.
Exemples
- Soit la droite d'équations cartésienne $(d):2x+3y-9=0$.
On a $2x+3y-9=0$ $\Leftrightarrow$ $y=-\dfrac{2}{3}x+3$, l'équation réduite de $(d)$ est $y=-\dfrac{2}{3}x+3$. - La droite $(d)$ posséde aussi comme équation cartésienne $-4x-6y+18=0$, on a $-4x-6y+18=0$ $\Leftrightarrow$ $y=-\dfrac{2}{3}x+3$
Remarque
Une droite $(d)$ non parallèle à l'axe des ordonnées, admet une infinité d'équations cartésiennes, mais possède qu'une seule équation réduite.
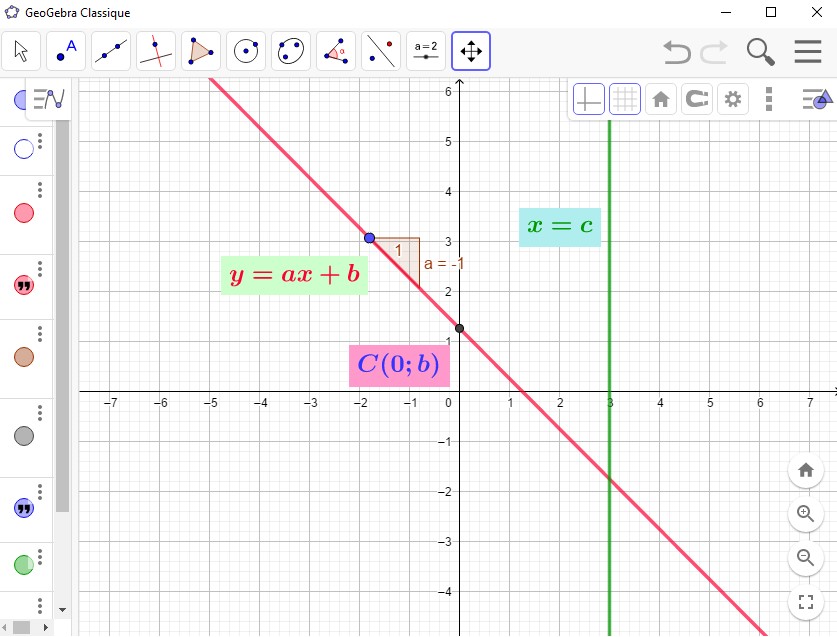
- Plaçons nous dans un repère $(O;\overrightarrow{i};\overrightarrow{j})$.
Si $\Delta$ est non parallèle à l'axe des ordonnées, alors nous savons d'aprés le théorème sur les équations cartésiennes que $(d):ax+by+c=0$ avec $\overrightarrow{u}(-b;a)$.
le vecteur $\overrightarrow{u}$ n'est pas colinéaire au vecteur $\overrightarrow{j}$, donc $\det(\overrightarrow{u},\overrightarrow{j})\not=0$ $\Leftrightarrow$ $\begin{array}{|cc|}-b&0\\a&1\\ \end{array}\not=0$ $\Leftrightarrow$ $b\not=0$.
Donc on $ax+by+c=0$ $\Leftrightarrow$ $by=-ax-c$ $\Leftrightarrow$ $y=-\dfrac{a}{b}x-\dfrac{c}{b}$.
L'équation $y=-\dfrac{a}{b}x-\dfrac{c}{b}$ est du type $y=mx+p$, cette équation s'appelle équation réduite de $\Delta$. - Si $\Delta$ est parallèle à l'axe des ordonnées le vecteur $\overrightarrow{u}$ est pas colinéaire au vecteur $\overrightarrow{j}$, donc $\det(\overrightarrow{u},\overrightarrow{j})=0$
$\Leftrightarrow$ $\begin{array}{|cc|}-b&0\\a&1\\ \end{array}=0$ $\Leftrightarrow$ $b=0$. De plus le vecteur $\overrightarrow{u}\not=\vec{0}$, donc $a\not=0$
Donc on $ax+by+c=0$ $\Leftrightarrow$ $ax+c=0$ $\Leftrightarrow$ $x=-\dfrac{c}{a}$.
Définition.
Soit $(d)$ la droite d'équation $y=$$m$$x+p$. Le nombre m est appelé coefficient directeur de la droite $(d)$ et le nombre $p$ est l'ordonnée à l'origine de cette droite.
Propriété.
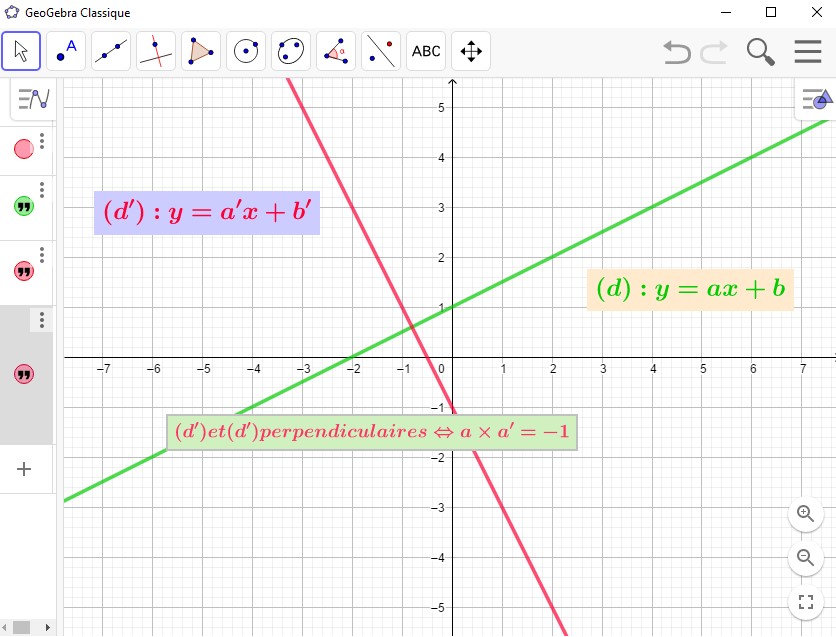
- Soit $\Delta$ une droite ayant pour équation réduite l'équation: $y=ax+b$.
Pour tout point $A$ et tout point $B$ de $\Delta$ avec $A(x_A;y_A)$ et $B(x_B;y_B)$ on a:
$a=\dfrac{y_B-y_A}{x_B-x_A}$. - Soit deux droites $(d):y=ax+b$ et $(d'):y=a'x+b'$.
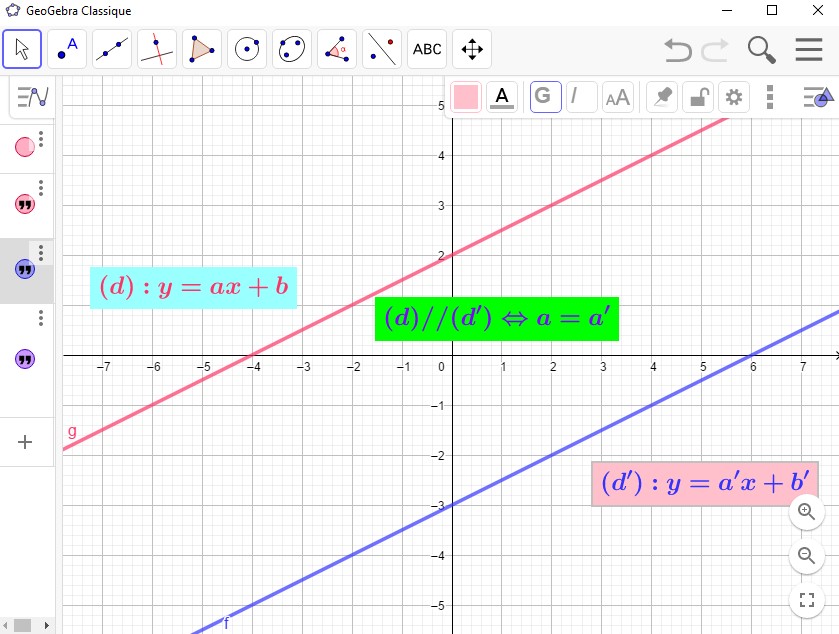
Les droites $(d)$ et $(d')$ sont parallèles si et seulemnt si $a=a'$. - Soit deux droites $(d):y=ax+b$ et $(d'):y=a'x+b'$.
Les droites $(d)$ et $(d')$ sont perpendiculaires si et seulemnt si $a\times a'=-1$.
Exercices
Déterminer l'équation réduite des droites suivantes:
- La droite $\Delta$ passant par $A(-5;2)$ et $B(-1;4)$.
- La droite $(d)$ passant par $C(1;2)$ est parallèle à la droite $(d'):y=-2x+3$.
- La droite $(\delta)$ passant par $D(0;3)$ est perpendiculaire à $(\delta'):y=\dfrac{1}{3}x+1$.
- La droite $\Delta$ passant par $A(-5;2)$ et $B(-1;4)$.
Calculons le coéfficient directeur de la droite $\Delta=(AB)$. on a $a=\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{4-2}{-1-(-5)}=\dfrac{2}{4}=\dfrac{1}{2}$.
Donc la droite $\Delta$ apour équation réduite $y=\dfrac{1}{2}x+b$, recherchons le nombre (ordonnée à l'origine).
Par exemple $A(-5;2)\in\Delta$, donc $y_A=\dfrac{1}{2}x_A+b$ $\Leftrightarrow$ $2=\dfrac{-5}{2}+b$ $\Leftrightarrow$ $b=2+\dfrac{5}{2}=\dfrac{9}{2}$.
Donc l'équation réduite de $\Delta$ est $y=\dfrac{1}{2}x+\dfrac{9}{2}$. - La droite $(d)$ passant par $C(1;2)$ est parallèle à la droite $(d'):y=-2x+3$.
Les droites $(d):y=ax+b$ et $(d'):y=-2x+3$ sont parallèles donc $a=-2$, et donc $(d):y=-2x+b$.
Déterminons le nombre $b$. Nous savons que $C(1;2)\in (d)$, donc $y_C=-2x_c+b$ $\Leftrightarrow$ $2=-2\times 1+b$ $\Leftrightarrow$ $b=4$.
Donc l'équation réduite de $(d)$ est $y=-2x+4$. - La droite $\delta$ passant par $D(0;3)$ est perpendiculaires à $(\delta'):y=\dfrac{1}{3}x+1$.
Les droites $(\delta):y=ax+b$ et $(\delta'):y=\dfrac{1}{3}x+1$ sont perpendiculaires donc $a\times\dfrac{1}{3}=-1$, et donc $a=-3$ ce qui veut dire que $(d):y=-3x+b$.
Déterminons le nombre $b$. Nous savons que $D(0;3)\in (\delta)$, donc $y_D=-3x_D+b$ $\Leftrightarrow$ $3=-3\times 0+b$ $\Leftrightarrow$ $b=3$.
Donc l'équation réduite de $(\delta)$ est $y=-3x+3$.
Activités autour de l'équation réduite d'une droite du plan.
Définition.
Deux vecteurs non nuls $\overrightarrow{u}$ et $\overrightarrow{v}$ sont dit colinéaires si et seulement si, il existe un nombre réel $k$ tel que $\overrightarrow{u}=k\times\overrightarrow{v}$.
Par convention le vecteur nul est colinéaire à tous les vecteurs.
Propriété.
Dans un repère quelconque, deux vecteurs $\overrightarrow{u}(x;y)$ et $\overrightarrow{v}(x';y')$ sont colinéaire si et seulement si on a: $x\times y'-x'\times y=0.$
Vocabulaire.
Soit dans un repére $\mathcal{R}(O;\vec{i};\vec{j})$ les vecteurs $\overrightarrow{u}\begin{pmatrix} x\\ y \\ \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} x'\\y' \\ \end{pmatrix}$.
Le nombre $x\times y'-x'\times y$ est appelé déterminant des vecteur $\vec{u}$ et $\vec{v}$ dans le repère $\mathcal{R}$.
On le note $\det(\overrightarrow{u},\overrightarrow{v})$ ou encore
$\begin{array}{|cc|}
x&x'\\
y&y'\\
\end{array}.$
Exercice.
$\overrightarrow{u}\begin{pmatrix} 10\\ -23 \\ \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} -6\\ 17 \\ \end{pmatrix}$. $\det(\overrightarrow{u},\overrightarrow{v})=\begin{array}{|cc|}10&-6\\-23&17\\\end{array}=10\times17-(-23)\times(-6)=170-138=32\not=0.$ Donc $\overrightarrow{u}$ et $\overrightarrow{u}$ ne sont pas colinéaires.Droite définie par un point et un vecteur directeur.
La droite $\mathcal{D}$ passant par $A$ et de vecteur $\overrightarrow{u}$ directeur est l'ensemble des points $M$ du plan tels que les vecteurs $\overrightarrow{AM}$ et $\overrightarrow{u}$ soient colinéaires.
Théorème.
Dans un repère quelconque $\mathcal{R}=(O;\overrightarrow{i};\overrightarrow{j})$ on a:
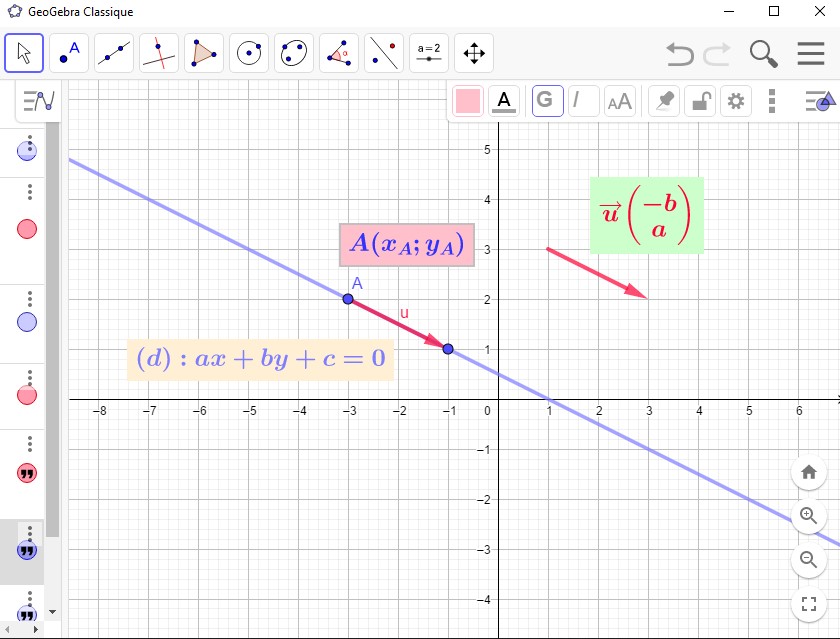
Exercices.
Donner une équation cartésienne de la droite $\Delta$, définie par: